Slicer

The Slicer component of Polytope is the main innovative contribution of this software. It contains a novel slicing algorithm which supports non-orthogonal slicing across ordered axes. This new algorithm is highly versatile, working on a number of different axis types and datacubes of arbitrarily high dimensions.

The concept behind the slicing algorithm is to successively slice the requested shapes' polytopes along each axis in the natural axis ordering until we are left with a list of all points contained in the shape.

Slicing Algorithm

To keep track of which points in the datacube are found during the data extraction process, the slicing algorithm builds an index tree. This index tree is built iteratively using the following method:

take input polytopes from requested shape

for axis in datacube:

    find polytopes defined on that axis
    for polytope in found polytopes:

        find extents of polytope on axis
        extract indices between extents from the datacube
        add extracted indices as children to the index tree
        for axis index in extracted indices:

            slice polytope along axis index to get lower-dimensional polytope

    update list of polytopes by list of sliced lower-dimensional polytopes

Note that the innermost for loop contains a special slicing step, which is the step that makes non-orthogonal slicing possible in Polytope.

Slicing Step

The slicing step used in Polytope is based on computational geometry concepts. The idea behind it is conceptually easy to understand and is shown in the figure below.

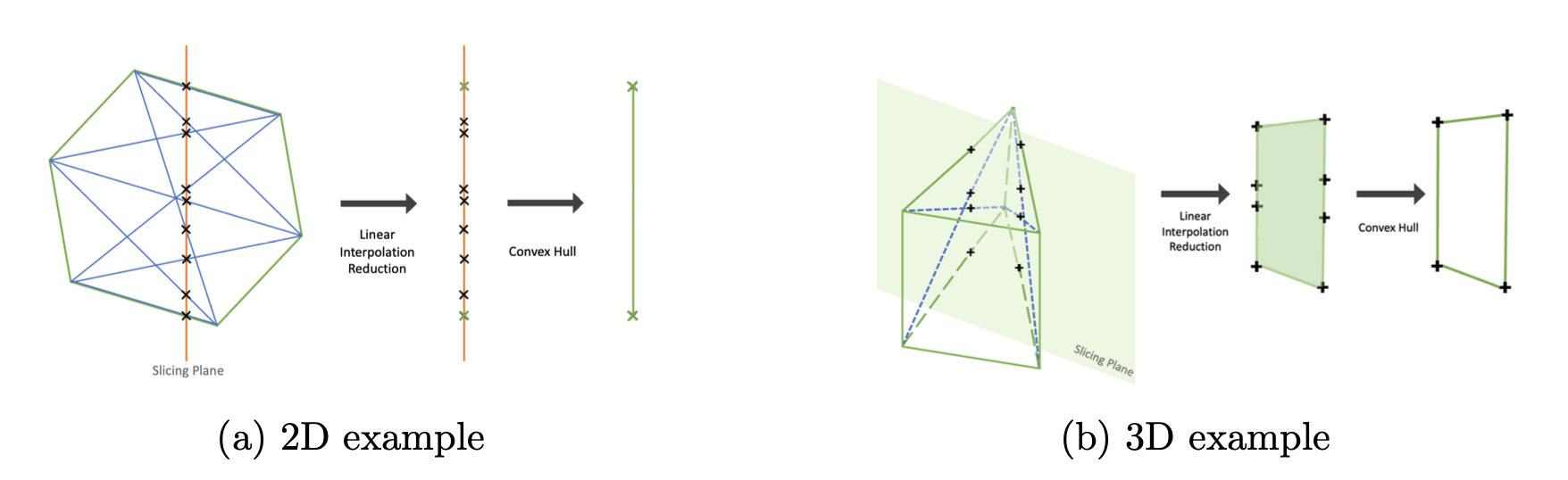
In words, this slicing step can be summarised as follows. First, all vertices in the polytope are separated into two distinct groups, each group consisting of points on either side of the slice plane. The algorithm then linearly interpolates between each pair of vertices where one vertex comes from one vertex group and the other from the other. For each pair of vertices, this gives an interpolated point which lies on the slice plane. Once this is done for all pairs, the obtained interpolated points define a lower-dimensional polytope on the slice plane. This polytope is in fact the wanted intersection of the original polytope with the slice plane. This thus concludes the slicing step.